Using laser distance meters in bright sun

MichaelNeyses

Hi Roger, I agree to all of it. As a landscape designer I do a lot of field work all by myself and since using the Leica Disto D8 all my work goes very easy with this tool. It just shows you a magnified picture on a small screen with crosshairs on the target and you dont nessesarily have to see the laser dot! Also, it calculates the elevation from your position and even transfers the results via bluetooth into your notebook. So you cover 2 of the required 3 dimensions very easy and very precise. Regretably there is no app for iphones as far as I know.

Gaieus

I also have a Bosch meter and it has a function to measure the shortest or longest route you are "sweeping through". Here are two, quick sketches what it does:

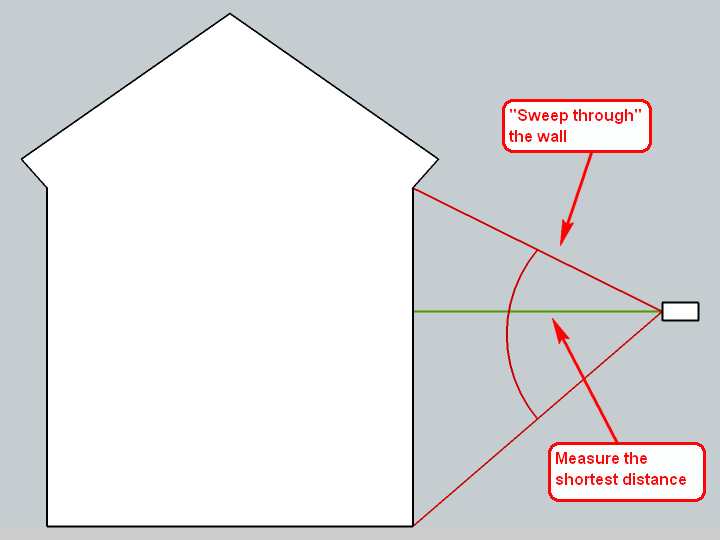
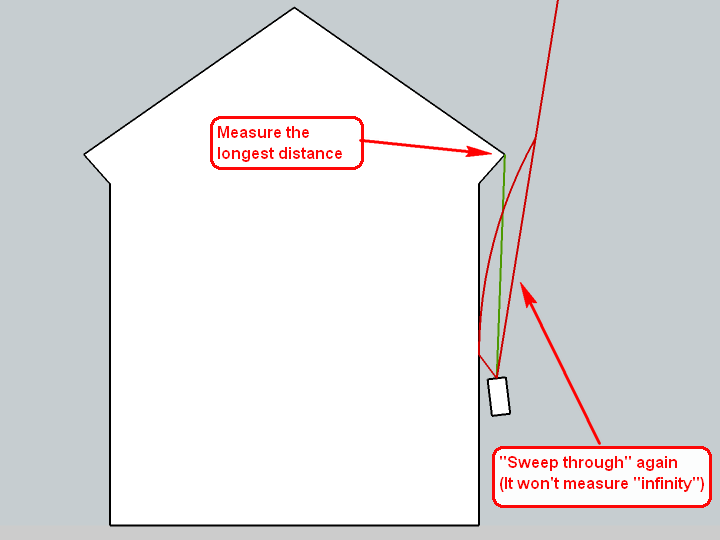
These methods are very handy when I cannot see the small, red dot of the laser scanner (which can indeed happen especially during light daytime on sunny surfaces).

I also have a stick of 1.5 metres long which I use to put my scanner on top when measuring the heights of buildings. This way I do not need to lean down to measure from the ground or measure twice (once up and once down from eye/measure height) to add the two values. Basically I start from a footprint, PP it up to 150 cms - then make the measurements and only add what I measure then.

mitcorb

Hi, Roger:
I fully appreciate your reply to my reply, especially on the economics. And I was aware that the Scanstation would represent a "significant capital outlay", to use a bland euphemistic phrase.

@Gaieus: That method is enlightening. Similarly Leica lets you do a Pythagorean process to arrive at building heights, or other distances. And, as you pointed out, without an established steady station point (top end of stick) the data can be worthless.

bjornkn

So what if the walls are not perfectly straight?
Lots of buildings have tapering walls, like Inca buildings, fortresses etc, and many have walls skewed by time/age and bad foundations, like the tower in Pisa etc.
Pythagoras won't help much then, will it?
I'm sure the Leica Disto D8 is a very useful tool, that can also do some angle measurements afaik, but will it be enough power/precision for such situations?
And with a price tag a lot higher (at least in this country ~US$1400) than the tgi3D/PhotoScan I know what I would have chosen But a cheap Bosch laser would probably be quite useful for measuring a reference distance. So far I have gotten enough precision with a 5m tape measure.

A bit OT:
A little while ago I saw a TV program from a volcanic rift (?) in Ethopia(?) where the team wanted to make a 3D scan of the extremely hot rift which puffed out toxic gases all the time. They rigged the laser scanner on a steel cable crossing the rift, and lowered it down to make the scan. They had to give up after a while, but they did get some parts of it 3D scanned. I can't help but smiling a little at their efforts, when they could have used the KISS principle and easily/safely gotten good results using PhotoScan (or similar software like PhotoModeler)

Gaieus

@mitcorb said:

Similarly Leica lets you do a Pythagorean process to arrive at building heights, or other distances.

Yeah, I wished I could get one of those but mine does not do Pythagoras. Of course, I can do it if I really need to

@bjornkn said:

Lots of buildings have tapering walls, like Inca buildings, fortresses etc, and many have walls skewed by time/age and bad foundations, like the tower in Pisa etc.

That's true however the majority of buildings are (fortunately) rectangular/vertical (more or less). If not, we get out our secondary school geometry books again and do some calculations.

bjornkn

@gaieus said:

That's true however the majority of buildings are (fortunately) rectangular/vertical (more or less). If not, we get out our secondary school geometry books again and do some calculations.
Wonder how those formulas look?

Gaieus

The book are in the attic ATM. I should get them down one day...

Roger

SOH-CAH-TOA:

Sine = Opposite ÷ Hypotenuse
Cosine = Adjacent ÷ Hypotenuse
Tangent = Opposite ÷ Adjacent

or

Some Old Hippy Caught Another Hippy Trippin' On Acid

Roger

@gaieus said:

I also have a Bosch meter and it has a function to measure the shortest or longest route you are "sweeping through". Here are two, quick sketches what it does:

DOH! Thanks, I don't remember seeing this in the instruction sheet. But then the whole thing looked so simple that I tossed the instruction without reading. Thanks Gaieus.

Gaieus

Well, devices of even the same brand can be very different so there may not be this function on yours. Yet of course looking it up would be best.

bjornkn

@Roger :
Afaik sin/cos/tan only works on right-angled triangles, and so do the Pythagoras rule a^2+b^2=c^2 - or here : a=sqr(c^2-b^2)
That's why I was so interested in the formulas in Gaieus' books. Too bad they are in the attic

BTW, did you get that iPhone theodolite to work with any precision?

Roger

Bjorn, any triangle can be divided into two right triangles, each of which can be solved by pythagoras or sohcahtoa.

bjornkn

@roger said:

Bjorn, any triangle can be divided into two right triangles, each of which can be solved by pythagoras or sohcahtoa.

Yes, as long as you know some angles?
Or if you measure from 2 positions?

TIG

While we are on 'formulas'...

If you know two sides of any triangle and the angle between them then you can find the length of the other side opposite that angle using the Cosine Rule
a^2 = b^2 + c^2 - 2bc*cosA
can be rearranged to give the side a thus...
a = sqrt(b^2 + c^2 - 2bc*cosA)
Notes:
Side 'a' is opposite angle 'A'.
There are obviously the other two versions of the equation for the two other sides, but you can give them the reference you want so you always find 'a' without needing to have these in memory!

The Sine Rule works for any two angles and one related side, from which you can find the another side
a / sinA = b / sinB = c / sinC = D
which can be rearranged to give the side a thus...
a = b * sinA / sinB
Notes:
Side 'a' is opposite angle 'A' and so on.
The ratios are all equal to D, which is the diameter of the circle that passes through all of the three vertices of the triangle - the radius of that circle is D/2.
To find the area of any triangle where you know two sides and the angle between them use
Area = a * b * sinC / 2

Roger

Folding stick
My folding meter stick with distance measure on top

Long stick
Stick unfolded - the distance (outer edge to outer edge) of the two yellow reflective tapes is 3ft.

Laser target bar hung magnetically on wall corner. Reflective tape is 1 ft long and entire black bar is 22 inches.

Neodymium magnets
This is the back of the target bar. The circles are neodymium super magnets affixed with double sided tape. There are also holes in the bar that can be used with push pins, nails, strings, picture hooks, and clamps.

This is the stick with compass

Distance meter mounted on stick
Compass remove and distance meter in place.

bjornkn

@tig said:

While we are on 'formulas'...

If you know two sides of any triangle and the angle between them then you can find the length of the other side opposite that angle using the Cosine Rule

Exactly!
But you need to know one angle (which may be 90 degrees) and 2 sides to calculate the length of the third, right?
With only 2 sides and no angle you can't know the length of the third side?
But if the wall is vertical (90 degrees) you can calculate without using sin/cos, but just the a^2+b^2=c^2?

bjornkn

Is there a built-in level in the Bosch laser then?

Roger

@bjornkn said:

Is there a built-in level in the Bosch laser then?

I am designing and building an accessory to attach a level and a small monocular and the whole device will clip to my meter/yard/walking stick.

Roger

@bjornkn said:

@roger said:

Bjorn, any triangle can be divided into two right triangles, each of which can be solved by pythagoras or sohcahtoa.

Yes, as long as you know some angles?
Or if you measure from 2 positions?

Two angles with the enclosed side or two sides and the enclosed angle. And if you know one angle to begin with and divide the triangle into two right triangles you will know your first angle, your second angle will be the right triangle (90 degrees). Then if you add known angle to 90 degrees and subtract the result from 180 degrees you know the third angle.

Roger

@bjornkn said:

Is there a built-in level in the Bosch laser then?

You did not fully understand the point of Gaieus' diagram and comments. As you sweep the meter up and down the distance reading will change. It starts out long reaches its shortest point and then gets long again. The angle where the distance is shortest is a perpendicular to the wall. When the distance is the shortest, you have a 90 degree angle between the wall and the laser line.