Where lies the bug?

Chris Fullmer

Thats interesting Thom. Does V-Ray work with any scale components?

thomthom

@chris fullmer said:

Thats interesting Thom. Does V-Ray work with any scale components?

Yes. Normally scaled groups/components render just fine.

I wonder if any other render engines does the same thing. That'd be interesting to see as I'd get a clue to if the bug lies in the render engine or not.

thomthom

Trying desperately to debug this:

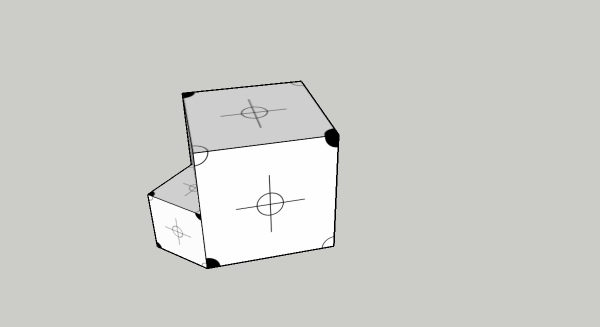
In this screenshot the two cubes are of the same definition. The large one is roated 45 degrees and scaled x2.0 manually.

.transformation.to_a returns this for the manually rotated and scaled box:
[1.4142135623731, -1.4142135623731, 0.0, 0.0, 1.4142135623731, 1.4142135623731, 0.0, 0.0, 0.0, 0.0, 2, 0.0, -16.3076205658699, 55.6776993060274, 0.0, 1.0]

If I then RotaScale the small box to fit the large one .transformation returns this:
[0.707106781186548, -0.707106781186548, 0.0, 0.0, 0.707106781186548, 0.707106781186548, -0.0, 0.0, 0.0, 0.0, 1.0, 0.0, -8.15381028293495, 27.8388496530137, 0.0, 0.5]

Every value of the RotaScaled component is half of the manually scaled and rotated component.
Isn't X,Y,Z co-ords somewhere in the transformation array as well?

free agent

do any of the other renderers experience this problem?

Pixero

Here's a snippet from my matrix plugin for MentalRay. Might help.
Its here if you want to see what the others do. http://www.pixero.com/files/JS_Place3dTexture.zip


        // Scale Matrix
        s[0] = Scale.x;
        s[1] = 0.0;
        s[2] = 0.0;
        s[3] = 0.0;

        s[4] = 0.0;
        s[5] = Scale.y;
        s[6] = 0.0;
        s[7] = 0.0;

        s[8] = 0.0;
        s[9] = 0.0;
        s[10] = Scale.z;
        s[11] = 0.0;

        s[12] = 0.0;
        s[13] = 0.0;
        s[14] = 0.0;
        s[15] = 1.0;


        // Translate Matrix
        t[0] = 1.0;
        t[1] = 0.0;
        t[2] = 0.0;
        t[3] = 0.0;

        t[4] = 0.0;
        t[5] = 1.0;
        t[6] = 0.0;
        t[7] = 0.0;

        t[8] = 0.0;
        t[9] = 0.0;
        t[10] = 1.0;
        t[11] = 0.0;

        t[12] = Translate.x;
        t[13] = Translate.y;
        t[14] = Translate.z;
        t[15] = 1.0;

thomthom

It appears that the last value in the 16x array is the transformation scale. And it looks like V-Ray doesn't handle scales that aren't 1.0.
No I need a way to normalize the transformation data.

Pixero

It might have to do with the order you do the various transforms.
The correct order would be:
Scale
Rotate
Translate

thomthom

Swapping to t = t_scale * t_rotation didn't work either.

Doing two separate transformation operations didn't help either.
model.active_entities.transform_entities(t_scale, model.selection) model.active_entities.transform_entities(t_rotation, model.selection)

thomthom

@pixero said:

The correct order would be:
Scale
Rotate
Translate

Why does the order matter?

What if an object is manipulated by different tools independently - first rotated then scaled?

I make two transformations and then combine them before I apply them to the selection.

t_scale = Geom::Transformation.scaling(@reference_point1.position, scale) # 3D t_rotation = Geom::Transformation.rotation(@reference_point1.position, v3, angle) t = t_rotation * t_scale model.active_entities.transform_entities(t, model.selection)

Pixero

@unknownuser said:

Why does the order matter?

Thats what I learned.
Try Googling for: transformation matrices order
Here is just one link http://msdn.microsoft.com/en-us/library/eews39w7.aspx

There is a great book called Complete Maya Programming Volume 2 with much info on matrices and other stuff that isnt neccessarily Maya specific.

Pixero

...or maybe it could be how they are multiplied: http://en.wikipedia.org/wiki/Matrix_multiplication

AdamB

@pixero said:

@unknownuser said:

Why does the order matter?

Thats what I learned.
Try Googling for: transformation matrices order
Here is just one link http://msdn.microsoft.com/en-us/library/eews39w7.aspx

The order does not matter. However, matrix transformations are not commutative (unlike for regular numbers).
eg Rotate * Scale is not the same as Scale * Rotate.

@thomthom said:

Trying desperately to debug this:

.transformation.to_a returns this for the manually rotated and scaled box:
[1.4142135623731, -1.4142135623731, 0.0, 0.0, 1.4142135623731, 1.4142135623731, 0.0, 0.0, 0.0, 0.0, 2, 0.0, -16.3076205658699, 55.6776993060274, 0.0, 1.0]

If I then RotaScale the small box to fit the large one .transformation returns this:
[0.707106781186548, -0.707106781186548, 0.0, 0.0, 0.707106781186548, 0.707106781186548, -0.0, 0.0, 0.0, 0.0, 1.0, 0.0, -8.15381028293495, 27.8388496530137, 0.0, 0.5]

Every value of the RotaScaled component is half of the manually scaled and rotated component.
Isn't X,Y,Z co-ords somewhere in the transformation array as well?

Yeah, I came across this too. Looks like SU (very naughtily) stores the scale in the W component of the 4th column. Its typically 1.0, so I guess they thought nobody would notice! So you need to set it to 1.0 explicitly.

Also check you 3 axes are all at right-anglers to each other (orthogonal). Your numbers above look good eg 1.414.. is square root of 2.0 (good) and then its 0.707.. which is reciprocal 2^0.5

Adam

thomthom

@adamb said:

Yeah, I came across this too. Looks like SU (very naughtily) stores the scale in the W component of the 4th column. Its typically 1.0, so I guess they thought nobody would notice! So you need to set it to 1.0 explicitly.

But then I need to scale up all the other values as well, right? If I didn't wouldn't I end up with a completely misplaced entity?

@adamb said:

Also check you 3 axes are all at right-anglers to each other (orthogonal). Your numbers above look good eg 1.414.. is square root of 2.0 (good) and then its 0.707.. which is reciprocal 2^0.5

Isn't this an rounding issue for when it converts the units to strings? The script only rotates and uniformly scales - so it shouldn't mess with the axis. (unless there's some underlying mechanism I'm not aware of?)

thomthom

I seem to have found a work around, normalizing the Scale transformation t_scale:

t_scale = Geom::Transformation.scaling(@reference_point1.position, scale) ts = 1 / t_scale.to_a[15] ta = t_scale.to_a.collect { |d| d * ts } t_scale = Geom::Transformation.new(ta)

Still, it'd be good to know what's really going on. And is there a better way to normalize the transformation.

I wonder if there's other plugins that might cause this problem with VfSU...

AdamB

Thats not going to work generally. What if I scaled by 2.0 in X, 5.0 in Y, and 8.0 in Z?
Just forget the SU hack of storing stuff in t[15]. Overwrite it with 1.0..

The 4x4 matrix you get back is really 4 vectors each of 4 elements laid out as:

[x axis direction and length, 0]
[y axis direction and length, 0]
[z axis direction and length, 0]
[origin , 1]

The last (4th) element of each is to all intents, not used.

BTW If you want to remove all scaling from matrix you need to make the length of each of those axes = 1.0

If t is the Geom::Transformation, then using the methods t.xaxis you get back a normalized vector.

m[0] = t.xaxis[0] m[1] = t.xaxis[1] m[2] = t.xaxis[2] m[3] = 0 m[4] = t.yaxis[0] m[5] = t.yaxis[1] m[6] = t.yaxis[2] m[7] = 0 m[8] = t.zaxis[0] m[9] = t.zaxis[1] m[10] = t.zaxis[2] m[11] = 0

gives you the transform with all scaling removed but leaving the rotation.

thomthom

@adamb said:

Thats not going to work generally. What if I scaled by 2.0 in X, 5.0 in Y, and 8.0 in Z?

For the purpose if the RotaScale plugin - it's all uniformly scaled.

@adamb said:

Just forget the SU hack of storing stuff in t[15]. Overwrite it with 1.0..

I'm not that familiar with this transformation matrix. And I'm not sure if I understand what you're saying here. If I just override t[15] to 1.0 I loose all scaling.

@adamb said:

gives you the transform with all scaling removed but leaving the rotation.

I actually do want the scaling.

AdamB

@thomthom said:

@adamb said:

Thats not going to work generally. What if I scaled by 2.0 in X, 5.0 in Y, and 8.0 in Z?

For the purpose if the RotaScale plugin - it's all uniformly scaled.

@adamb said:

Just forget the SU hack of storing stuff in t[15]. Overwrite it with 1.0..

I'm not that familiar with this transformation matrix. And I'm not sure if I understand what you're saying here. If I just override t[15] to 1.0 I loose all scaling.

Its meant to be 1.0 Its actually wrong not to be 1.0 but since the matrix is used for 3D and not 4D, they "get away with it".

@adamb said:

gives you the transform with all scaling removed but leaving the rotation.

I actually do want the scaling.

Aren't we going around in circles here? The blah.transform.to_a gets the correct transform for blah. I use it all the time in LightUp and it works fine. The only thing is, SU stores some uniform scale info in m[15]. If you want to apply this uniform scale then you could do:

m[0] = t.xaxis.length=m[15] ... ...

Perhaps its worth explaining that the scale of each axis is represented in the matrix as the length of the axis vector. So when you have X axis pointing along 1,0,0 and Y along 0,1,0 and Z along 0,0,1 then changing the length of those vectors becomes making those '1' the scale_factor, hence you'll see code that sets the diagonal of the matrix to scale_factor as Pixero suggested.

Adam

fredo6

Tom,

Sorry to pop up in this. I may have missed something.
Do you wish to rotate and scale individual cubes (which is what I guess), or the whole selection?

thomthom

@unknownuser said:

Tom,

Sorry to pop up in this. I may have missed something.
Do you wish to rotate and scale individual cubes (which is what I guess), or the whole selection?

Whole selection. In regards to the RotaScale plugin: http://forums.sketchucation.com/viewtopic.php?f=180&t=19199
The plugin works, in SU at least - but the problem is that VfSU doesn't read the transformation of the groups/components properly. So the transformation data needs to be converted into the same as it would if you'd use native SU tools.

scottlininger

Thom,

Can you filter the weirdness down to a few lines of Ruby and post? Sounds like SketchUp is using one unused cell of the transform matrix to store some scale information. I have no idea why, but there's probably a legacy reason for it.