Comment faire une pomme diamant?
-
Encore une autre méthode pour faire ce polyèdre-étoilé-qui-doit-bien-avoir-un-petit-nom-plus-sympa-que-pomme-diamant, pas très rapide, mais qui a le mérite d'avoir l'élégance de faire apparaitre cette belle forme d'un coup.
Le problème récurent dans la construction est l'apparition de faces à l'intérieur du volume. Pour faciliter l'accès à ces faces, j'ai utilisé les calques (c'est bien la première fois que je trouve un usage valable aux calques
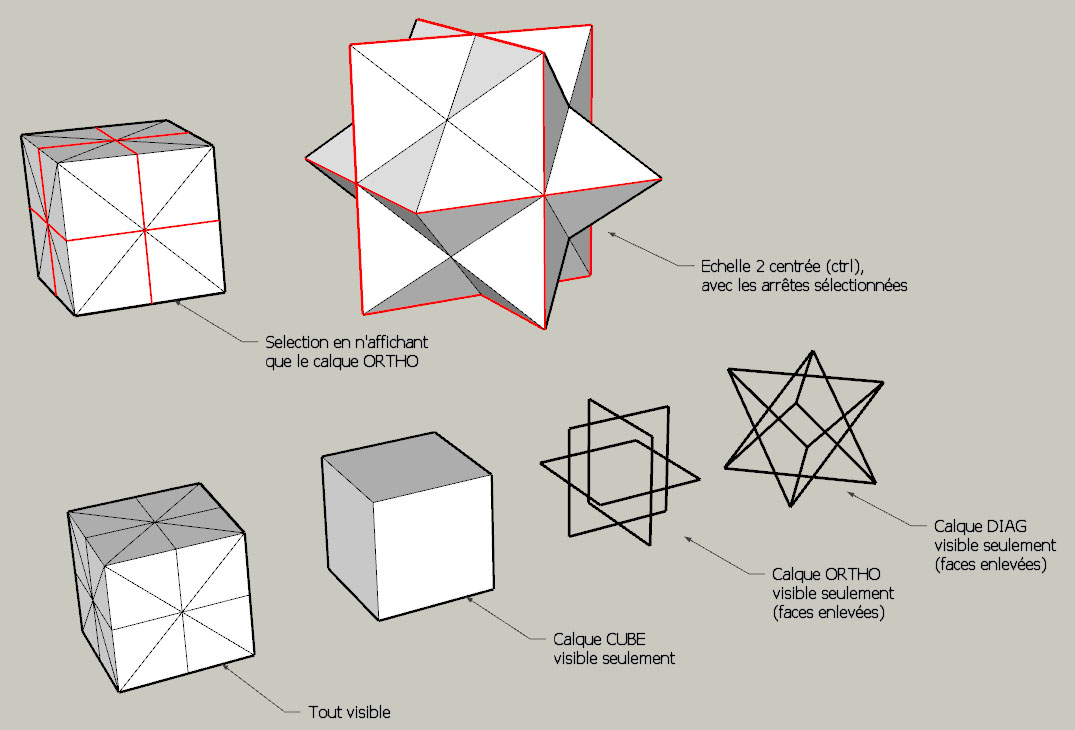
).- Dans un calque "CUBE" on trace le cube de base
- Dans un calque "ORTHO" on traces les verticales et horizontales au milieu de chaque face
- Dans un calque "DIAG" on trace les diagonales de chaque face
- En n'affichant qu'un seul calque, on voit les faces intérieures créées par ces tracés. Il suffit d'enlever toutes les faces (mais pas les arrêtes) des calques "ORTHO" et "DIAG" et toutes les faces intérieures ont disparu !
- En n'affichant que le calque "ORTHO" on sélectionne toutes les arrêtes
- Sans dé-sélectionner, on affiche tout et on fait une échelle de 2 centrée (avec ctrl)
Et voilà !!
Diam_V6.skp
-
Une autre construction
Et c'est un solide puisque pas de faces intérieures!B peut aussi être une rotation de A !
H le symétrique des facettes G , F par rapport à un plan horizontal
pourrait être remplacé par deux simples rotations mais il faut "inverser" l'orientation des faces (blues / blanches) après les rotations!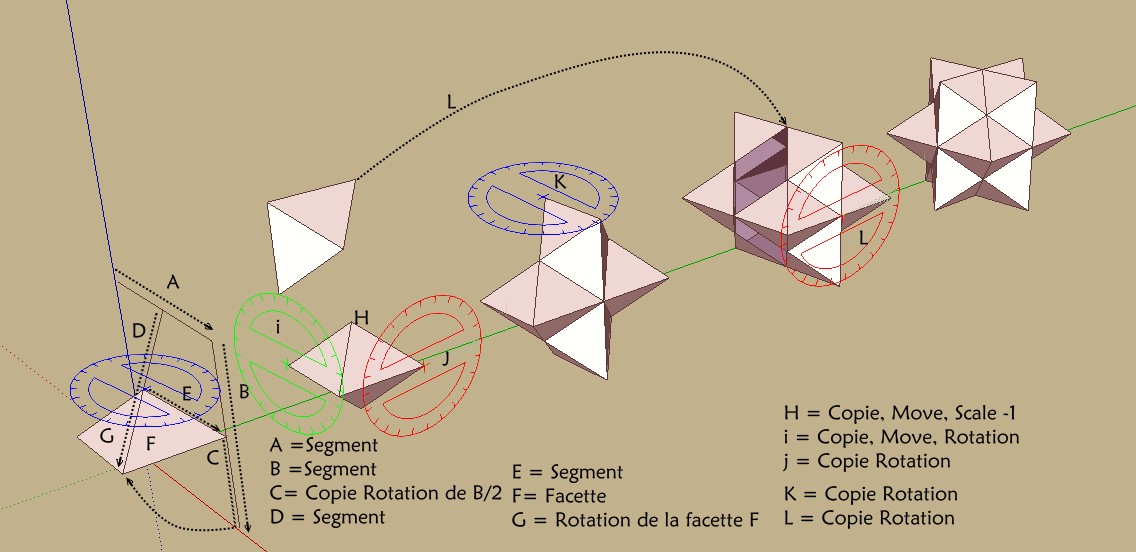
-
Bonjour.
Pilou, je t'ai simplifié le début et j'ai exécuté les rotations des copies d'une autre façon.
Voir le fichier SU suivant:
Pomme diamant 3.skp
En fait, il y a probablement autant de façon de faire qu'il y a de participants à ce forum, sinon plus.Un petit défi (challenge) pourrait être de trouver la méthode qui demande le moins d'opérations pour réaliser cette forme.
Salutations.
-
@ Jean: Croisement de posts, je vais voir si c'était la même chose!
Vu : même départ, suite un peu différente
Dans ma solution je n'ai pas besoin de "retourner" de face bleue!Encore plus simple
16 étapes (une boîte de sélection étant prise comme une étape)
-
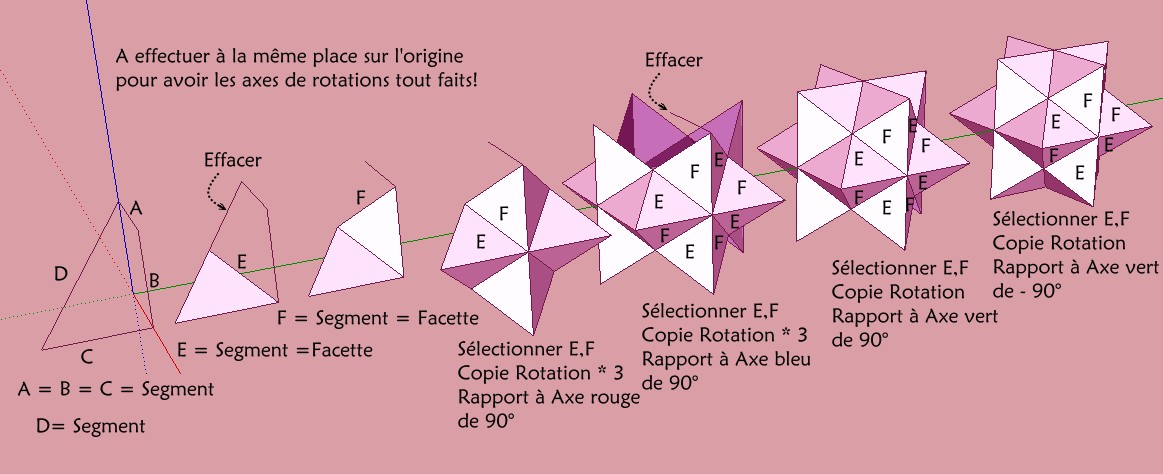
Une autre méthode?
-
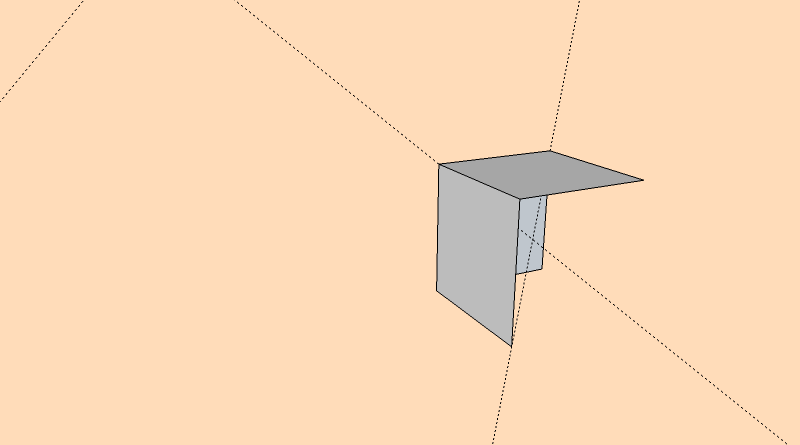
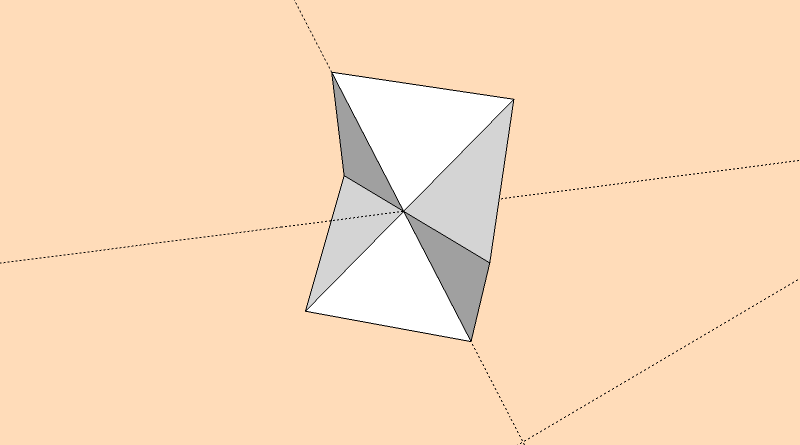
Super!
On y pense jamais au déplacement dynamique!
-
@daredevil said:
Encore une autre méthode pour faire ce polyèdre-étoilé-qui-doit-bien-avoir-un-petit-nom-plus-sympa-que-pomme-diamant, ...
Il s'agirait d'un dodécaèdre rhombique étoilé.
-
-
Solution "orthodoxe" en Mover!
Je n'ai que des groupes et que des axes par défaut!
-
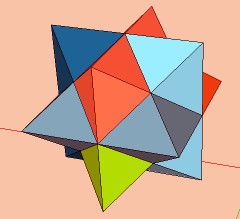
@gilles said:
@daredevil said:
Encore une autre méthode pour faire ce polyèdre-étoilé-qui-doit-bien-avoir-un-petit-nom-plus-sympa-que-pomme-diamant, ...
Il s'agirait d'un dodécaèdre rhombique étoilé.
Ben oui !!! un dodécaèdre rhombique étoilé
Merci Gilles
Le dodécaèdre rhombique est un volume que j'aime bien parce qu'il pave l'espace
Maintenant, je l'aime encore plus parce qu'il est le parent de notre dodécaèdre rhombique étoilé !! @unknownuser said:
un granatoèdre?
J'aime moins, ça raconte pas sa forme...
[Edit]
Aller, encore un bon point de plus pour le dodécaèdre rhombique étoilé : il pave lui aussi l'espace comme son père le dodécaèdre rhombique et son grand père le cube !!!
(Trouvé dans l'article dont Gilles a donné le lien) -
Bonjour.
@gilles said:
@daredevil said:
Encore une autre méthode pour faire ce polyèdre-étoilé-qui-doit-bien-avoir-un-petit-nom-plus-sympa-que-pomme-diamant, ...
Il s'agirait d'un dodécaèdre rhombique étoilé.
Exact.
En Anglais: Stellated Rhombic Dodecahedron.
Voir cette page:
Je n'ai pas trouvé son équivalent en Français.
Aussi appelé Polyèdre d'Escher. Voir cette page:
http://www.math.ens.fr/culturemath/video/Dupas-polyedres/herbier/rhombique.htm
Ou Cascade d'Escher. Voir cette page:
En effet, c'est le polyèdre qu'on retrouve à la partie supérieure des deux tours dans cette oeuvre bien connue de Escher.
Et, finalement, la façon la plus rapide d'obtenir cette figure est d'insérer le composant nommé 36 sided polyhedrondu Bonus Pack "Shapes" que Google SketchUp proposait sur sa page de téléchargement pour SketchUp 6. Vous allez le retrouver sur l'entrepôt 3D (3D Warehouse) si vous tapez exactement 36 sided polyhedron.
Salutations.
-
@jean lemire said:
Un petit défi (challenge) pourrait être de trouver la méthode qui demande le moins d'opérations pour réaliser cette forme.
oui, en fait c'était un peu l'idée de départ de ma question, quand j'ai lancé ce sujet ...
"comment réaliser ce polyèdre plus vite que les cuisiniers! "
Advertisement