[Résolu] défi:dodecaèdre (problème de méthode?)
-
bonjour,
j'essaye de faire un dodecaèdre avec su8,
en theorie ça devrait être très simple; c'est un volume fait avec un même plan, le pentagone, placé à tous les axes.google image : "great dodecahedron"
seulement au bout d'une demi_heure, je n'y étais pas arrivé...

parce qu'un volume aussi exact ne tolère pas l'à-peu-près
et manipuler un plan à 5 cotés c'est très complexe!
j'y arrive pas
problême de methode? en tout cas, si vous trouver des ruses, je suis tout ouie !!
philippe
-
Salut regarde sa si sa peut aider.http://www.youtube.com/watch?v=mtErWSfwtTc


-
@pho0o0 said:
bonjour,
j'essaye de faire un dodecahèdre avec su8,problême de methode? en tout cas, si vous trouver des ruses, je suis tout ouie !!

philippe
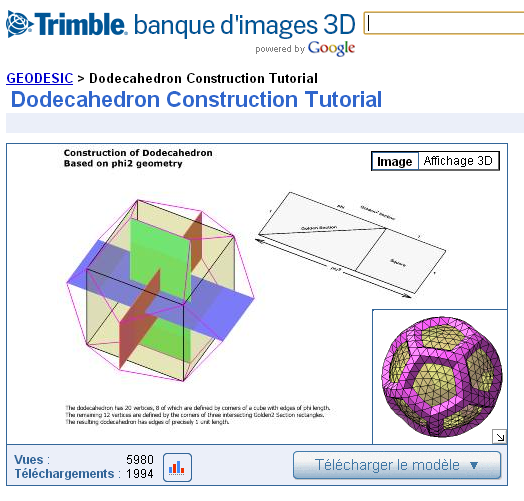
%(#008000)[bonjour Philippe
Je te propose de jeter un oeil aux travaux de TaffGoch qui realise ces types dessins de facon magistrale !
adresse : http://sketchup.google.com/3dwarehouse/search?uq=0058532540730737055623450&scoring=m&start=36
Salutations
chri]
-
@eddy said:
Salut regarde sa si sa peut aider.http://www.youtube.com/watch?v=mtErWSfwtTc
Bien vu l'utilisation du rectangle d'or ! Je n'y avais jamais pensé...
-
Malin le gars!

Enfin ça m'étonnerait que ce soit lui qui ait trouvé que l'angle du dodécaèdre
soit la diagonale du rectangle d'or!
Il doit falloir remonter un peu plus loin dans le temps!
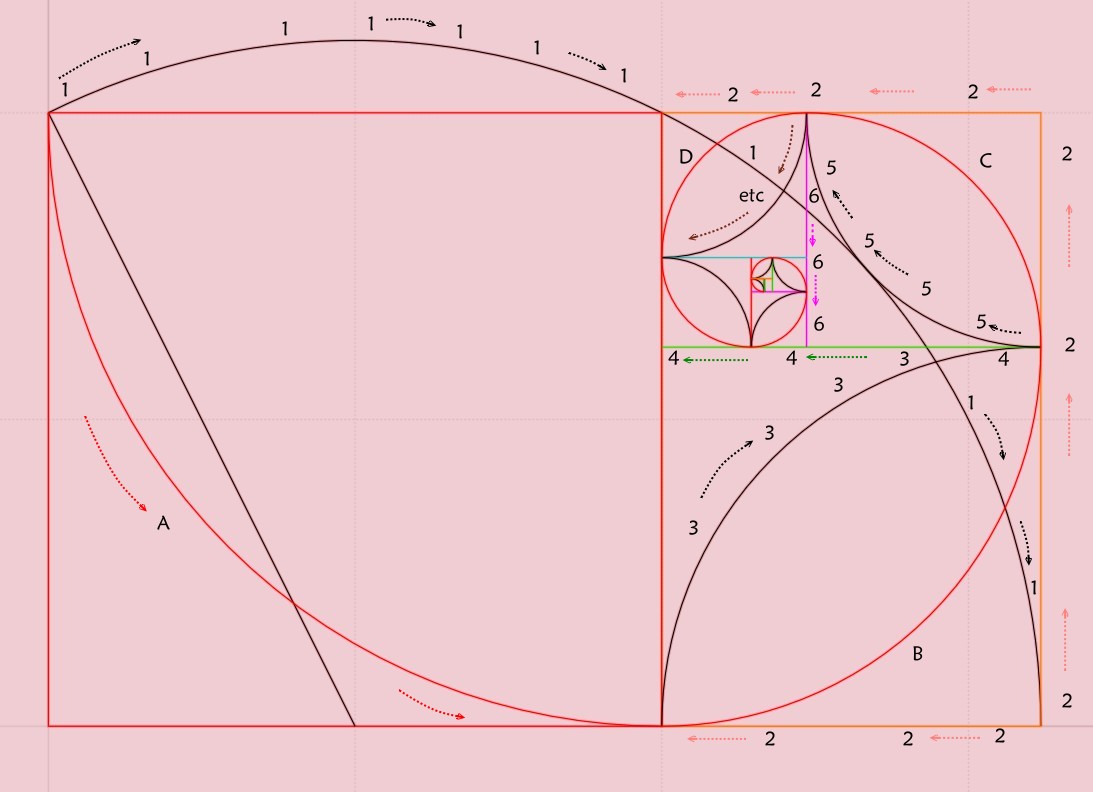
On le retrouve partout ce rectangle d'or

Voici comment le construire
 Ainsi que sa spirale
Ainsi que sa spirale 
-
En tout cas un bon exercice pour manipuler les lignes d'aide et le rapporteur

-
L'abus de H peut nuire à la santé, ce sera donc un dodécaèdre !

-
Pour faire un grand dodécaèdre, je commencerai par faire un icosaèdre :
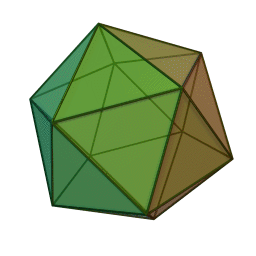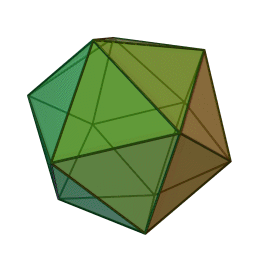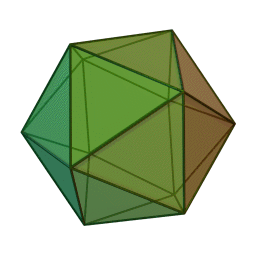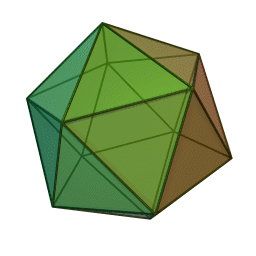
... et pour faire un icosaèdre, je commencerai par faire un dodécaèdre (parce que la technique qu'on a vu est super simple
 )
)
En fait l'un est le dual de l'autre, c'est à dire que les sommets de l'un se trouvent aux centres des faces de l'autre.
Donc, en reliant les centres du dodécaèdre on construit un icosaèdre, mais comme SketchUp crée toutes les faces, il va créer des faces intérieures pentagolales. Une fois toutes les faces triangulaires de l'icosaèdre supprimées, il restera la grand dodécaèdre.
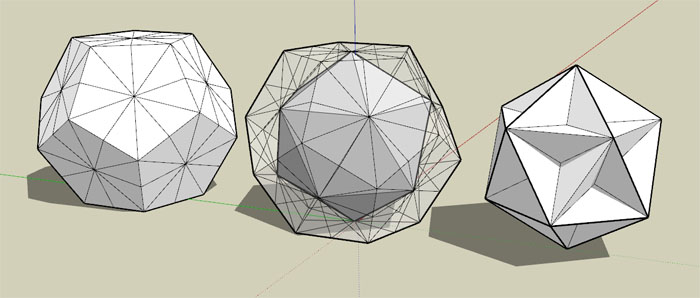
-
merci de votre aide!
j'ai regardé vos liens, et ça m'a instruis de les refaire sur SU8...mais je dois encore creuser la question pour trouver une methode simple pour realiser un
'grand dodecaedre'

différent d'un
'dodecaedre'
Vos liens m'ont permis néanmoins d'aborder le problème différement;
(peut-être que j'y arriverai...)
ça reste un vrai défi!

-
(merci Franky, pour le H; c'est corrigé
 )
)merci aux contributeurs pour leurs idées!
du coup, j'ai trouvé le moyen de faire très simple à partir de tout ça:Petit tuto rapide
je construis mon icosaèdre avec trois rectangle d'or

etape 2
je reunis les sommets


etape 3
je selectionne les faces et je les supprime !

parce que comme Daredevil le rappelle juste au-dessus, SU construit toutes les faces:

et voilà

-
Super


Un dernier petit truc : à la fin, tout sélectionner et bouton droit pour créer les arrêtes aux intersections des faces qui se croisent (intersection avec la sélection je crois...) -
BEAU TRAVAIL D'EQUIPE !
Chri
-
Advertisement







