Strange result of a substraction

Jim

Much has been written about floating point errors.

Basically, floating point numbers can not be accurately represented in binary.

Dan Rathbun

@macgile said:

i have tested with a = a + b the result is same

That is because the Ruby interpreter converts
a += b
to
a = a + b
before the expression is evaluated.

voljanko

@unknownuser said:

i dont compare anything !!!
i have tested with a = a + b the result is same

I just meant that is always good to avoid considering floats as exact numbers.

macgile

@dan rathbun said:

@macgile said:

i have tested with a = a + b the result is same

That is because the Ruby interpreter converts
a += b
to
a = a + b
before the expression is evaluated.

i dont understand your explanation Dan !!!!

macgile

@voljanko said:

@unknownuser said:

i dont compare anything !!!
i have tested with a = a + b the result is same

I just meant that is always good to avoid considering floats as exact numbers.

oh yes

I thought the result would be near to 0 and not of 4.

voljanko

Try to add some number,you will see that is zero and not 4.

Dan Rathbun

A singleton method to increment a float a, by an argument arg, to dec number of decimal places. (It defaults to 1 decimal place.)

a = 9.0
def a.incr( arg = 1.0, dec = 1 )
  dec = dec.to_i
  arg = round( arg.to_f * 10**dec  )
  # self is object a
  temp =( round( self * 10**dec ) + arg ).to_f
  self =( temp / 10**dec )
end

use it like:
a = 9.0 b = -1.8 a.incr(b)

Jim

@macgile said:

I thought the result would be near to 0 and not of 4.

macguile,

4.44089209850063e-016

The e-016 at the end of the number means to move the decimal place 16 places to the left - making the actual number:

0.0000000000000000444089209850063

or very nearly zero. The reason the result is not exactly zero is due to floating point errors as linked above.

macgile

@dan rathbun said:

A singleton method to increment a float a, by an argument arg, to dec number of decimal places. (It defaults to 1 decimal place.)

a = 9.0
> def a.incr( arg = 1.0, dec = 1 )
>   dec = dec.to_i
>   arg = round( arg.to_f * 10**dec  )
>   # self is object a
>   temp =( round( self * 10**dec ) + arg ).to_f
>   self =( temp / 10**dec )
> end

use it like:
a = 9.0 b = -1.8 a.incr(b)

THANK for this solution Dan

Best Regard

macgile

@jim said:

@macgile said:

I thought the result would be near to 0 and not of 4.

macguile,

4.44089209850063e-016

The e-016 at the end of the number means to move the decimal place 16 places to the left - making the actual number:

0.0000000000000000444089209850063

or very nearly zero. The reason the result is not exactly zero is due to floating point errors as linked above.

thank i nderstand now

regard

thomthom

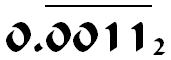
The Floating-Point Guide - What Every Programmer Should Know About Floating-Point Arithmetic

Aims to provide both short and simple answers to the common recurring questions of novice programmers about floating-point numbers not 'adding up' correctly, and more in-depth information about how IEEE 754 floats work, when and how to use them correctly, and what to use instead when they are not appropriate.

(floating-point-gui.de)