La véritable courbette! :)
-
Vérification...
Hum hum
De deux choses l'une, l'autre c'est le soleil!
Soit ma construction est fausse (je doute) soit le True Bend n'utilise pas ce rabattement...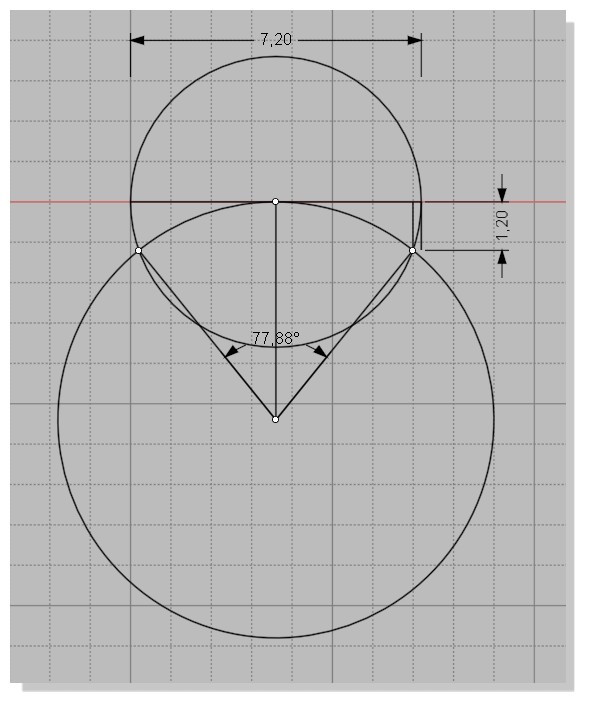
-
Bonjour
@camsone said:
, il faut que je puisse rentrer la valeur du bend.
Penses-tu pouvoir ajouter une colonne avec le bend dans ton tableau? Ça serait l'idéal
Pour avoir le bend, dans E4, tu écris =B$2*B4/PI()^2 et tu tires la formule vers le bas. Je ne sais pas à quoi cela correspond exactement, géométriquement parlant, mais bon, cela donne les mêmes résultats que Truebend pour des angles de 360, 180, 90 et 45°. Dans cette formule intervient le rayon (= 720/bêta), et le rapport bêta/(2 pi).
@ plus
-
@pilou said:
[attachment=3:3d5xa09k]<!-- ia3 -->2cercles_bis.jpg<!-- ia3 -->[/attachment:3d5xa09k]
Merci Pilou pour tes recherches. Sur cette construction, la distance de l'arc 123 ne fait pas 720 mais un eu plus de 734, ce n'est donc pas cette géométrie que fait TrueBend.
@ciscoo said:
Pour avoir le bend, dans E4, tu écris =B$2*B4/PI()^2 et tu tires la formule vers le bas.
Impec! en effet, Bend = longueur de l'objet x angle / 2pi², c'est la formule que je cherchais.
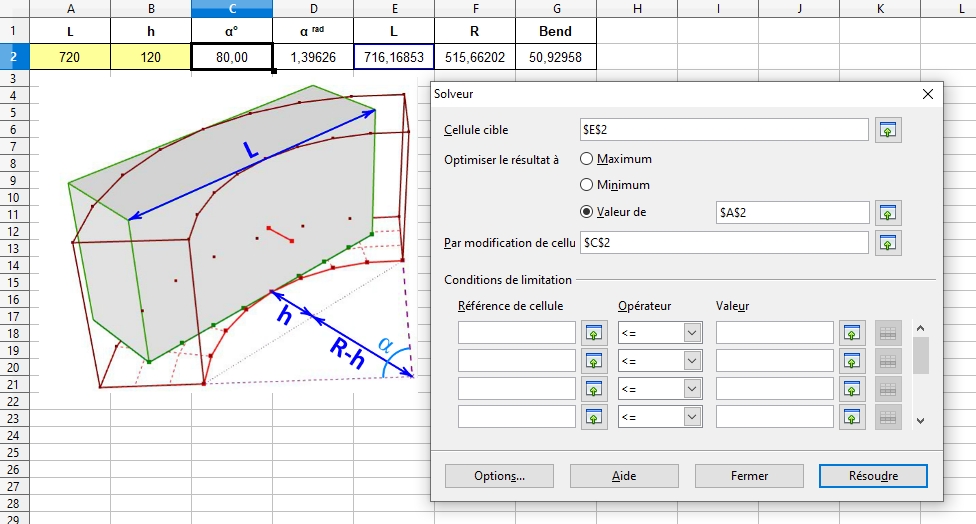
Dans openoffice j'ai essayé de résoudre le problème grâce au solveur (=calculateur), en lui demandant de modifier la valeur de l'angle jusqu'à ce que E2 soit très proche de L2. Mais malheureusement il ne sait résoudre que des équations linéaires :[attachment=2:3d5xa09k]<!-- ia2 -->img 7.jpg<!-- ia2 -->[/attachment:3d5xa09k]
[attachment=1:3d5xa09k]<!-- ia1 -->img 8.jpg<!-- ia1 -->[/attachment:3d5xa09k]La solution de l'itération à la main fonctionne bien qu'elle soit un peu longue.
Je joins mon fichier si ça intéresse qqn.
[attachment=0:3d5xa09k]<!-- ia0 -->SU TrueBend 2 .xls<!-- ia0 -->[/attachment:3d5xa09k]
-
Bonjour
Dans Excel, pour ne pas avoir à le faire de proche en proche, tu peux le faire avec la valeur cible :
Données --> Analyse de scénarios -> Valeur cible
Dans la nouvelle fenêtre
Cellule à définir : C4
Valeur à atteindre : 360
Cellule à modifier : A4@ plus
-
Yes! Et pour openoffice il existe une extension qui permet de calculer les équations non linéaires : (https://extensions.openoffice.org/fr/project/solver-nonlinear-programming-beta)
Un peu laborieux tout ça mais ça fait le job au final!
Merci Pilou et Ciscoo!
-
Bon à savoir le solveur non linéaire!

Sinon à l'ancienne sans solveur...sans résolution...qu'en géométrie....
Les degrés et le cercle ne sont que des cotes de vérification...
Que donne le solveur ?
J'aurais sans doute pu avoir une courbe plus précise mais en 2 coup de cuillères à pot faut pas trop en demander!
-
Bonsoir Pilou
@pilou said:
Bon à savoir le solveur non linéaire!

Sinon à l'ancienne sans solveur...sans résolution...qu'en géométrie....
Les degrés et le cercle ne sont que des cotes de vérification...Les grecs faisaient presque tout avec de la géométrie... dans ce domaine.
@pilou said:
Que donne le solveur ?
Un angle au centre de 79,5366°, un rayon de 518,68 mm et un bend de 50,634 mm.
@ plus
-
@pilou said:
Que donne le solveur ?
angle = 79,5366561275801
rayon = 518,666024672295
bend = 50,6346079188187 -
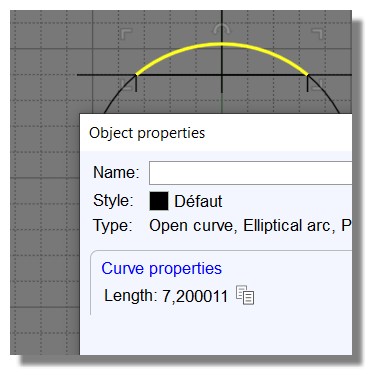
Le rayon du dessus du solveur donne 7,1999997 dans mon logiciel 3D favori à moi!

J'étais arrivé en classique à 7,2000011 mais n'avais fini!
-
Bon, je ne pourrais pas aller plus loin!

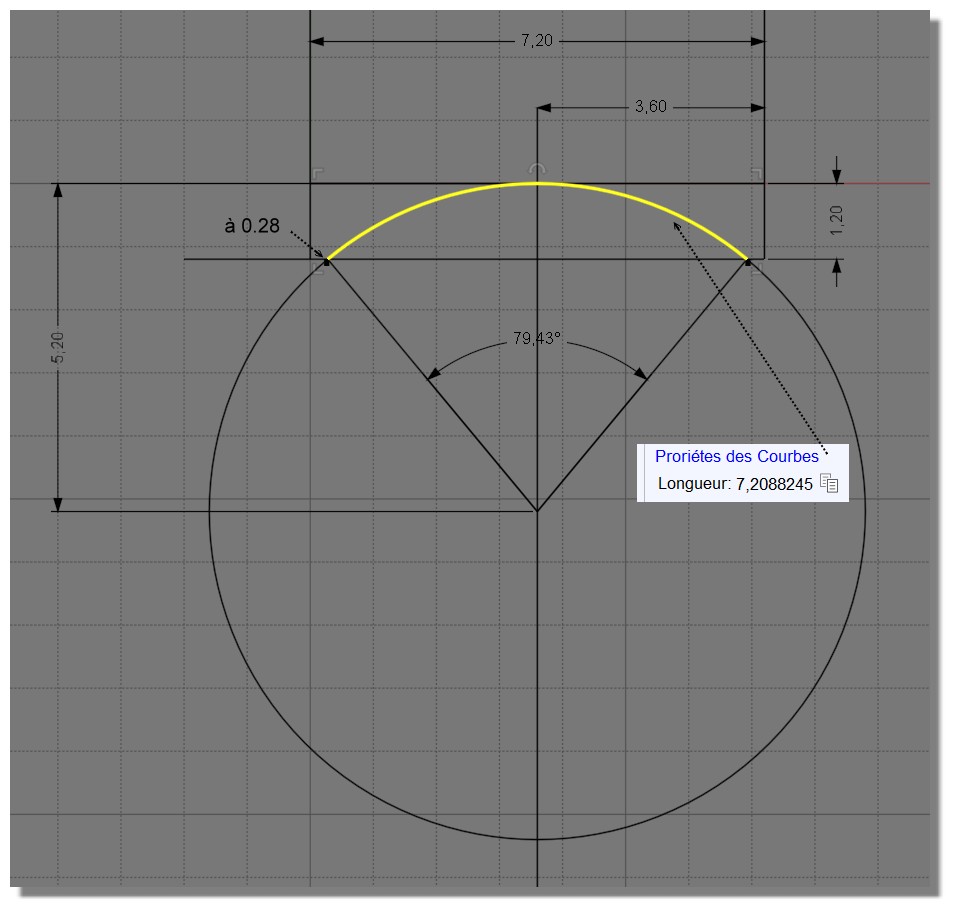
un rayon de 5.1866606 me donne l'arc de 7.2000000 ( 7 chiffres après la virgule) précison maxi du programme utilisé! Je n'ai pas remis dans la sauce tomate pour avoir le Bend obtenu...
Le "à 0.28" est en fait 0.2821716

A comparer avec le solveur!
angle = 79,5366561275801°
rayon = 5,18666024672295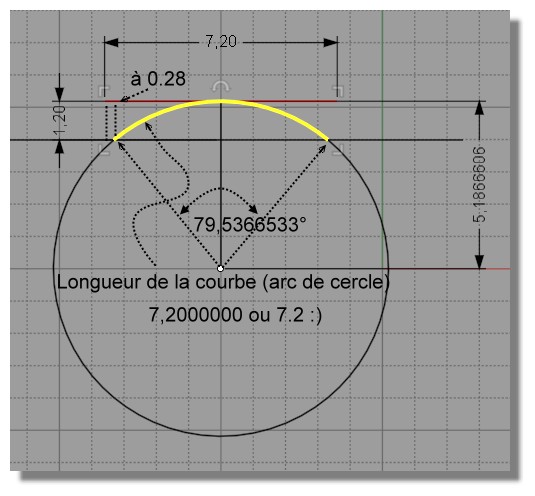
Advertisement







