How to orient component in space using ruby?
-
Hy!
I want to move a simple component from one position to another and orient it in space. I know the position of all corners of a face. See attached image.
Please help me with this. Moving the component is the easy part. But there is the alignment which is tricky. pt1 is located in origin (axis don't show up in exported image)
thanks
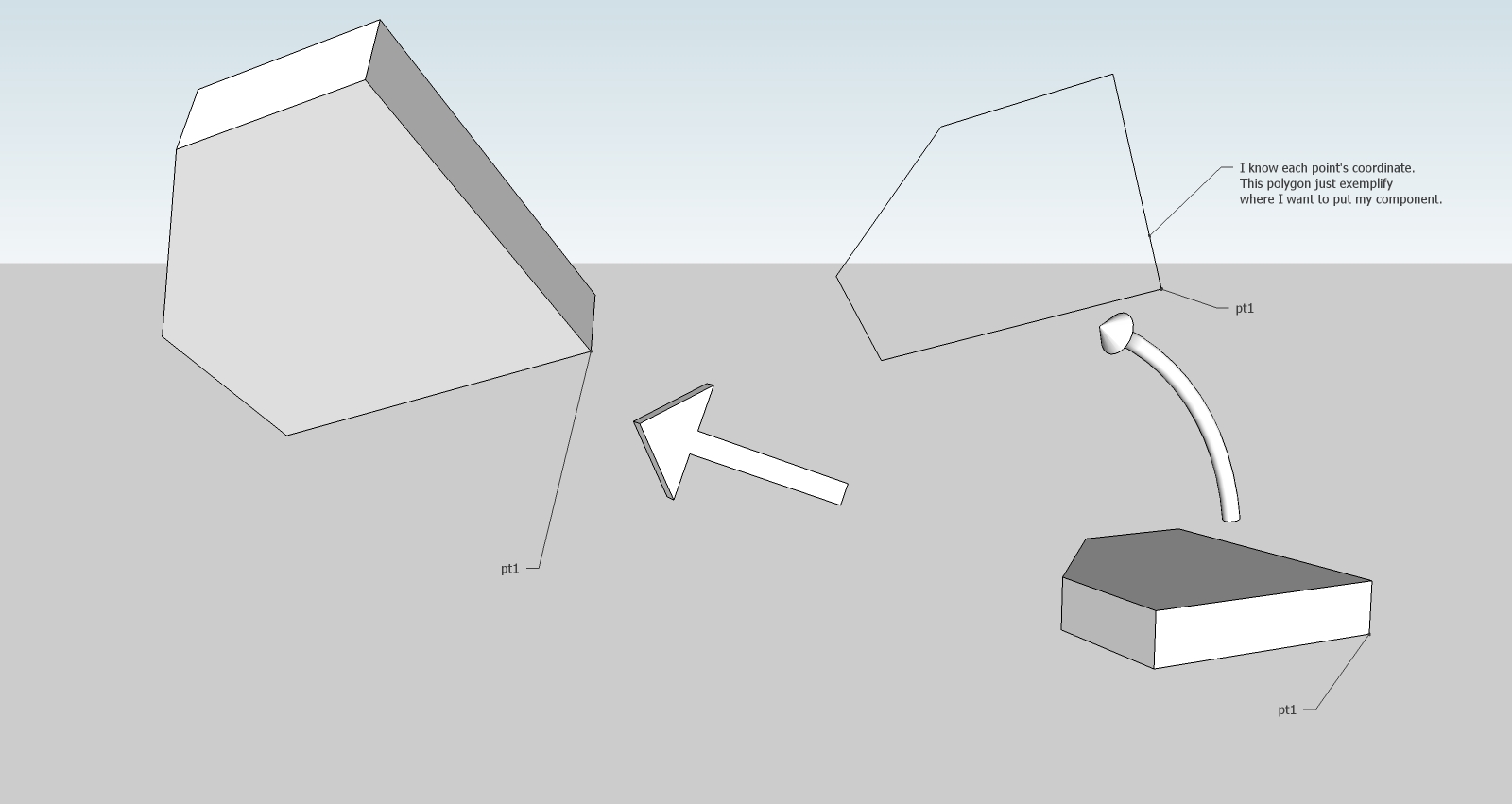
-
How do you define where you want it to move? Is it meeting up with another face? or is it based on the orientation of other geometry?
Chris
-
@chris fullmer said:
How do you define where you want it to move? Is it meeting up with another face? or is it based on the orientation of other geometry?
Chris
I know the position in space of each vertex of the face.
-
Didier Bur has yet made a good one

@unknownuser said:
Align selection in 3D, starting from a clicked XYZ axis system to a target XYZ plane (Autocad-like). PDF doc included.
-
Yeah, but this is a function gets used in lots of ways other than just aligning components.
Here is how you can do it if you know the new 3dpoint in space that you want to move the component axis to, and you need to know the axes for the new location. These can be found depending on what defines where you are moving the component to. But this code is useful:
t = Geom::Transformation.axes point, xaxis, yaxis, zaxis component.transformation = tpoint is the new 3d location that component axis will be moved to.
xaxis is the vector that represents the new x direction fo the component
yaxis is the vector that represents the new y direction fo the component
zaxis is the vector that represents the new z direction fo the componentI can diagram it better if that doesn't make sense. I just learned how to use this transformation today, and I like it.
Chris
-
You don't need to know the positions of where the component is, but where it is going to move to.
-
@chris fullmer said:
You don't need to know the positions of where the component is, but where it is going to move to.
Whow! thanks
 In fact is really simple. And I don't need the position of each vertex, just component's final orientation.
In fact is really simple. And I don't need the position of each vertex, just component's final orientation.
How about inferencing, Chris? Did you figured out? I finally understood how inference_lock works.
Thanks again, Chris! -
point = [0,0,0]
xaxis = [1,0,0]
yaxis = [0,1,0]
zaxis = [0,0,1]this represents the origin and the original axis. So take a component and move it off the origin, and rotate it all sorts of ways. Then select it and run this code:
comp = Sketchup.active_model.selection[0] point = [0,0,0] xaxis = [1,0,0] yaxis = [0,1,0] zaxis = [0,0,1] t = Geom::Transformation.axes point, xaxis, yaxis, zaxis comp.transformation = tThat will move any component, with any rotation put on it back to the origin. Now play around with the axis values. Use
zaxis = [0,0,-1]and you'll see it will flip your component upside down. So if you can supply yourt own 3d point and your own new coordinate axes, you can move/rotate it all in one shot.
Chris
-
oh good, I hope you get it. post again if its not working. And no, I haven't been able to get to the inference yet. Its tricky. And transformations are what keep me awake at night - literally! I need a good book on 3d transformations...
Chris
-
@chris fullmer said:
oh good, I hope you get it. post again if its not working. And no, I haven't been able to get to the inference yet. Its tricky. And transformations are what keep me awake at night - literally! I need a good book on 3d transformations...
Chris
Well, Chris you suddenly became my best friend ! I'll share my toys with you

When you will fully understand transformations, maybe you will share with us, because I still look at them something like this


-
Also, in case you know nothing about axes, like me, Fredo showed me that if you multiply 2 axes together, you get a perpendicular axis. This is helpful if you can find 2 axes, say the x and y, you can just multiply them together to get the z axis. Then you have all 3 axes needed for the transformation. It would look like this:
xaxis = Geom::Vector3d.new(10,-23,110) yaxis = Geom::Vector3d.new(23,52,9) zaxis = xaxis * yaxisGives the result of:
(-5927.0, 2440.0, 1049.0)for the zaxis.
Chris
Advertisement








