The Transformation Matrix

remus

I know a bit about matrices and transformation matrices.

Have you read the wiki article jim? Thatll be a good place to start to get the general idea about how matrices behave.

I'll do a quick word document with an explanation of them, give us 30 mins or so.

EDIT: just reread your post and im not sure how well any of the stuff i know will transfer over to ruby stuff, ill do it anyway

EDIT 2: i just realised what a large topic matrices are, and how long it would take to do a proper explanation. If you dont mind i wont do the word doc. Im happy to answer any queries you have about transformation matrices and matrices in general, though.

remus

I dont think its possible to extract both the scale and rotation in matrix form, as each operation is defined by a separate matrix. These 2 matrices are then multiplied to give you the final transformation.

To use a simple analogy, imagine we can define the final transformation as the number 12, trying to extract the scale and rotation is like saying "which numbers multiply to give us 12?" obviously theres a few different answers, so we cant say definitively.

If you could find one though, say the scale of the enlargement, you could then find the rotation with a bit of matrix based jiggery pokery.

Jim

So here's a bit of code to format the transformation array as a matrix. First, I should ask if I've got the matrix correct, or transposed?


class Geom;;Transformation
  def to_matrix
    a = self.to_a
    f = "%8.3f"
    l = [f, f, f, f].join("  ") + "\n"
    str =  sprintf l,  a[0], a[1], a[2], a[3]
    str += sprintf l,  a[4], a[5], a[6], a[7]
    str += sprintf l,  a[8], a[9], a[10], a[11]
    str += sprintf l,  a[12], a[13], a[14], a[15]
    str 
  end
end


Geom;;Transformation.new.to_matrix
   1.000     0.000     0.000     0.000
   0.000     1.000     0.000     0.000
   1.000     0.000     1.000     0.000
   0.000     0.000     0.000     1.000

A bit easier on the eyes. So what you see is the transformation matrix for a Group that is at the Origin, has no scaling, and no rotation.

Now, let's move the Group to position (3, 4, 5):


   1.000     0.000     0.000     0.000
   0.000     1.000     0.000     0.000
   0.000     0.000     1.000     0.000
   3.000     4.000     5.000     1.000

That's easy enough. Now move the Group back to the model Origin, and rotate it 45 deg around Z:


   0.707    -0.707     0.000     0.000
   0.707     0.707     0.000     0.000
   0.000     0.000     1.000     0.000
   0.000     0.000     0.000     1.000

Now, I need a minute to make sense of that... although I recognize the relationship of 45 and 0.707... O.K. below is the same matrix with 4 sets labeled; p, v1, v2, and v3.


   v1[0.707    -0.707     0.000]   0.000
   v2[0.707     0.707     0.000]   0.000
   v3[0.000     0.000     1.000]   0.000
    p[0.000     0.000     0.000]   1.000

The set labeled p is the Group's position in the model. The sets labeled v1, v2, and v3 represent the x, y, and z vectors for the Group. The following image [image 1] shows the physical representation of vectors v1, v2, and v3:

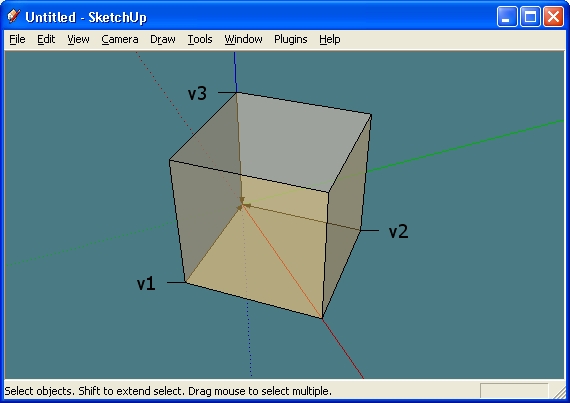
And if this is correct, we should be able to simply take the length of the vectors v1, v2, and v3 to get the x, y, and z axis scale. Let's test... O.K. that seems logical and appears to give the correct results.

So, for the getting the scale along each of the Group's axes, I get:


class Geom;;Transformation
  def xscale; Geom;;Vector3d.new(self.to_a[0, 3]).length; end
  def yscale; Geom;;Vector3d.new(self.to_a[4, 3]).length; end
  def zscale; Geom;;Vector3d.new(self.to_a[8, 3]).length; end
end

Which is in agreement with Whaat's solution also (although he used the length of vector formula.)

Note: this is a work in progress...

tbd

it still has bugs, but I am too sleepy now. maybe someone can see the problem with fresh eyes


module Geom
  class Transformation
    def scale_x;self.to_a[0..2].x;end
    def scale_y;self.to_a[4..6].y;end
    def scale_z;self.to_a[8..10].z;end
    
    def rot_x;180-Math.acos((xaxis*X_AXIS).y).radians;end
    def rot_y;Math.acos((yaxis*Y_AXIS).x).radians;end    
    def rot_z;180-Math.acos((zaxis*Z_AXIS).y).radians;end    
  end
end

t =  Sketchup.active_model.selection[0].transformation
p "%s %s %s" % [t.rot_x, t.rot_y, t.rot_z]

CPhillips

Could it also detect "flipped" transforms? When you do "flip along..." it does something to the transform. I never have been able to wrap my brain around it but AdamB wrote a explanation in this thread.

301 Moved Permanently

(www.sketchucation.com)

remus

In a standard matrix transformation any matrix which flips an object has a negative determinant, good bit about how to find the determinant of a matrix here.

Didier Bur

Hi Jim,

Here's what I found:

module Math
  def Math;;arcsin(x) 
    x = x % 1
    atan2(x,sqrt(1.0-x*x))
  end
end

class Geom;;Transformation
  def identity
    Geom;;Transformation.new([1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1])
  end

  def xscale
    ((Geom;;Vector3d.new 1,0,0).transform! self).length
  end

  def yscale
    ((Geom;;Vector3d.new 0,1,0).transform! self).length
  end

  def zscale
    ((Geom;;Vector3d.new 0,0,1).transform! self).length
  end

  def xrot
    Sketchup.format_angle(Math.atan2(self.to_a[9],self.to_a[10]))
  end

  def yrot
    Sketchup.format_angle(-Math.arcsin(self.to_a[8]))
  end

  def zrot
    Sketchup.format_angle(Math.atan2(self.to_a[4],self.to_a[0]))
  end
end

Hope this helps,

Jim

Didier, is your arcsin the same as Math::asin?

Didier Bur

Yes

Jim

Ok, good. I wasn't sure if asin was simply overlooked, or if you needed something different.